Prufer 序列的定义
$\rm Prufer$ 序列可以将一颗结点数为 $n$ 的有标号无根树用一个长度为 $n-2$
具体来说
- 选择一个编号最小的叶子节点
, 。 - 将这个叶子节点所连接的点的编号加入 $\rm Prufer$ 序列中
。 - 重复以上步骤 $n-2$ 次
, 。
这是某一颗点数为 $n$ 的有标号无根树的 $\rm Prufer$ 序列的构造过程
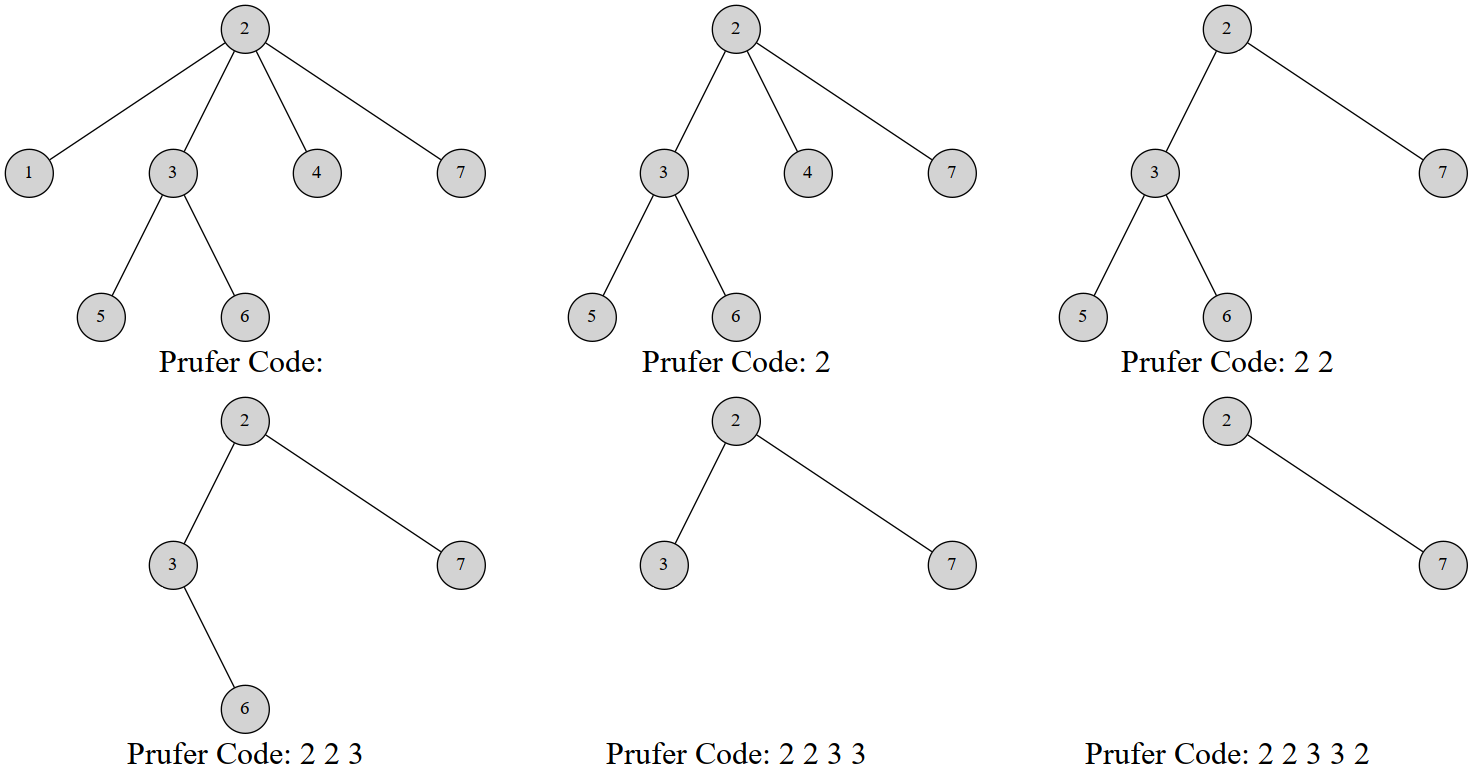
快速求解 Prufer 序列
由其过程
记录所有点的度数和一个指针 $p$ 指向编号最小的叶子节点
- 将 $p$ 指向的结点删除
, 。 - 如果产生了新的叶结点
, 。 , , , , 。 - 让 $p$ 自增直到遇见下一个叶结点为止
。 - 重复以上操作直到结点数为 $2$ 可以得到这棵树的 $\rm Prufer$ 序列
。
可以发现
总时间复杂度 $\Theta(n)$
快速还原 Prufer 序列
显然还是有一个堆优化的 $\Theta(n\log n)$ 做法
从前到后枚举 $\rm Prufer$ 序列中的每一个数
考虑以与之前构造 $\rm Prufer$ 序列相同的方法构造线性做法
记一个指针 $p$ 指向不在序列中的最小结点
显然
Prufer 序列的应用
Cayley 公式
完全图 $K_n$ 有 $n^{n-2}$ 颗生成树
。
证明方法很多
考虑到任何一个长度为 $n-2$ 的 $\rm Prufer$ 序列唯一对应一颗大小为 $n$ 的有标号无根树
限定度数的有标号无根树计数
求有 $n$ 个结点
考虑到一个点的度数为其在 $\rm Prufer$ 序列中出现次数 $+1$